在摘要中,他们认为新方法的期望搜索复杂度远远比之前大家所想的低:
本文重新审视了数据结构中最简单的问题之一:将元素插入开放寻址哈希表,以便以后能够用尽可能少的探测操作来检索元素。 我们证明,即使不随时间重新排序元素,也可以构建哈希表,其期望搜索复杂度(包括摊销(amortized)复杂度和最坏情况复杂度)远远优于之前认为可能实现的结果。 由此,我们推翻了姚期智开创性论文《Uniform Hashing is Optimal》中的核心猜想。我们所有的结果都有相应的下界。40年前的猜想
纽约市康奈尔大学科技校区(Cornell Tech)的Alex Conway表示:「这是一篇重要的论文。哈希表是我们拥有的最古老的数据结构之一,而且它们仍然是存储数据的最有效方式之一。」
然而,他表示关于它们如何工作的开放性问题仍然存在,这篇论文以令人惊讶的方式回答了其中几个问题。
哈希表在计算机领域已变得无处不在,这在一定程度上要归功于它们的简洁性和易用性。哈希表的设计允许用户执行三项基本操作:查询(搜索)、删除以及插入元素。最早的哈希表可追溯到1950年代初期,计算机科学家从那时起就一直在研究和使用它们。研究者们的一个目标是找出这些操作的速度限制。例如,新的搜索或插入操作最快能达到什么速度?
在哈希表中查找空位所需的时间,通常取决于哈希表的满载程度。满载程度可以用百分比来描述。例如,这个表是50%满的,那个表是90%满的。
但研究人员通常处理的是更高填充度的情况。因此,他们可能使用一个整数x来指定哈希表接近100%满的程度。如果x是100,那么表是99%满的。如果x是1,000,那么表是99.9%满的。这一填充度的衡量方式为评估查询或插入等操作所需时间提供了方便的标准。
研究人员早就知道,对于某些常见的哈希表,最坏情况下插入操作所需的时间——比如把某个元素放入最后剩余的空位——与x成正比。Kuszmaul说:「如果你的哈希表填充了99%,那么你可能需要检查大约100个位置才能找到一个空位。」
在1985年,姚期智(未来的图灵奖得主,清华「姚班之父」)在一篇论文中提出,对于具有特定属性的哈希表,查找一个元素或空位的最佳方法是随机遍历所有潜在位置,这种方法被称为均匀探测(uniform probing)。
他还指出,在最坏的情况下,查找最后一个空位时,所需时间永远不会优于x。
论文链接:
40年来,大多数计算机科学家都认为姚期智的猜想是对的。
然而,Krapivin并没有被这种传统观点所束缚,因为他根本不知道这一猜想。
他说:「做这个研究时,我并不知道姚期智的猜想」。
在Farach-Colton和Kuszmaul帮助下,Krapivin推翻了姚期智在40年前提出的猜想。
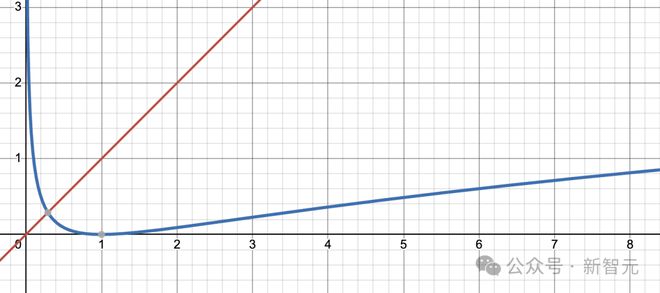
具体而言,全新的哈希表不依赖于均匀探测,而且就是姚期智所讨论的常见哈希表,但最优、不可超越的上限是(log x)²,而不是姚期智所猜想的x。
下图更直观的比较了两者复杂度,其中红色表示姚期智猜想的复杂度,蓝色表示新算法的复杂度。
而这一切都源于他偶然接触到的微指针论文。
卡内基梅隆大学的Guy Blelloch表示:「这个结果非常漂亮,因为它解决了一个经典问题。」
滑铁卢大学的Sepehr Assadi表示:「他们不仅仅是推翻了姚期智的猜想,他们还找到了问题的最佳答案。如果没有这个研究,我们可能还要等40年才能得到正确的答案。」
常数查询哈希表
除了推翻姚期智的猜想,这篇新论文还包含了更加令人惊讶的结果。
这与一个相关但稍有不同的情况有关:1985年,姚期智不仅研究了查询的最坏情况时间,还研究了所有可能查询的平均时间。他证明了:具有某些特性的哈希表——包括「贪婪」哈希表(即新元素必须放置在第一个可用位置的哈希表)——平均查询时间无法优于log x。
Farach-Colton、Krapivin和Kuszmaul想要验证这个限制是否同样适用于非贪心哈希表。
结果他们发现并不适用,并通过一个反例证明了这一点:他们构造了一个非贪心哈希表,其平均查询时间远远优于 log x,甚至完全不依赖于 x。
Farach-Colton解释道:「你会得到一个固定的数值,这只是一个常数,与哈希表的填充程度无关。」
也就是说,平均查询时间是恒定的,不受哈希表填充度的影响。
这一发现完全出乎意料,甚至连研究作者自己都感到惊讶。
Conway说道,团队的研究成果可能不会立即带来实际应用,但这并不重要。「更好理解这类数据结构很重要。你无法预见这样的研究何时会带来突破,从而在实际应用中取得更好的效果。」
主人公介绍
目前,Andrew Krapivin在剑桥大学攻读计算机科学硕士学位。之前,他在Rutgers大学荣誉学院(Honors College )攻读数学和计算机科学的双学位。因上文报道的研究工作,先后获得美国Goldwater奖学金和剑桥大学的丘吉尔奖学金。
参考资料:


还没有评论,来说两句吧...